图的操作与实现
要求
- 图的邻接表和邻接矩阵存储
- 建立下图的邻接表或邻接矩阵,并输出之;
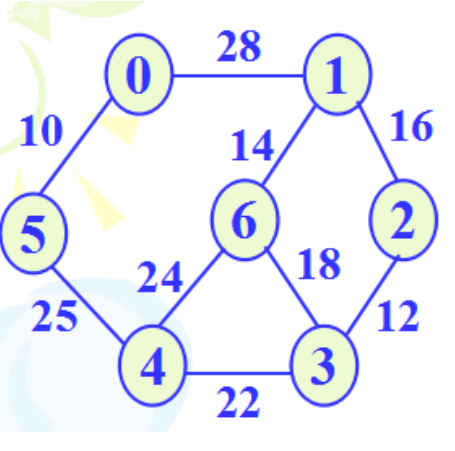
- 思路:
- 通过遍历邻接矩阵,采用头插法即可构造邻接表。
- 图的各种遍历算法实现
- 以0结点为起点实现上述图的深度优先和广度优先遍历算法;
- 思路:
- 用堆栈实现深度优先遍历,用队列实现广度优先遍历。
- 最小生成树的算法实现
- 利用普里姆(Prim)算法或克鲁斯卡尔(Kruskal)算法求上图的最小生成树,算法实现代码必需有注释。
- 思路:
- Prim:从0点出发每次取能到达的最小权重边,走完即为一颗最小生成树。
- 最短路径的算法实现
- 利用狄克斯特拉(Dijkstra)算法求上图中0结点到其它结点的最短路径,算法实现代码必须有注释。
- 思路:
- 循环每次计算到每一个点的最小距离并记录,然后取最小距离的那个点合并。
源代码
若以下显示需要登录,请刷新页面或点击此处下载。
思考
若只求带权有向图G中从顶点i到顶点j的最短路径,如何修改Dijkstra 算法来实现这一功能?
void Dijkstra_way(int first_point)
{
int* widget_list = new int[map_size]; //记录距离0的长度
for (int i = map_size; i--;)
{
widget_list[i] = INF;
adjList[i].weight = -1;
}
widget_list[first_point] = 0;
adjList[first_point].weight = 0;
for (int i = 1; i < map_size; ++i)
for (int j = map_size; j--;) //计算距离
if (adjList[j].weight >= 0)
for (node* node_p = adjList[j].next_p; node_p != NULL; node_p = node_p->next_p)
if (widget_list[j] + node_p->weight < widget_list[node_p->data])
{
widget_list[node_p->data] = widget_list[j] + node_p->weight;
adjList[node_p->data].weight = j;
}
cout << "<< Dijkstra 最短路径:" << endl;
coolQueue<int> stack;
for (int i = 0; i < map_size; ++i)
{
for (int j = i; j != first_point;)
{
stack.End_push(j);
j = adjList[j].weight;
}
cout << "<< " << first_point;
for (int pop_int = 0; stack.End_pop(pop_int);)
cout << " -> " << pop_int;
cout << endl;
stack.clear();
}
adjList_reflush();
}